Area of Square | What is Area of a Square Formula?

Area of Square

Area of Square:- The square’s size is the amount of square units required to make up the square. Also in order to calculate the square’s size then we look at how long its sides. Since all edges of the square are the same and its size is the product of the two edges. The most commonly used units to determine the size of a sq. meter are the square meters square feet, square inches or square inches, as well as square cm.

The square’s area can be determined using other dimensions, including the diagonal as well as the length that the rectangle has. We will try to learn more about the dimensions of the square on this article.

How do I calculate what is Area of Square?

A square is an open, two-dimensional shape that has four sides equal and four equally sized angles. Four sides on the square make up four angles at its vertex. The sides of a rectangle is its perimeter and the space filled by the rectangular shape is called the surface in the form of a square. It is an quadrilateral that has the following properties.

• Parallel sides on the opposite side.

• Each side is equal.

• All angles are 90o.

The shape of squares is all across the globe. Here are some of the most commonly seen objects that have the form of an square. The clock, chessboards and a blackboard tile, are just a few examples of the square.

The definition of Area in an area of

The square’s area is the measurement of the area or surface which it covers. It is the distance between its sides. Since the size of an area is the product of two edges, its measurement of area is shown as square units.

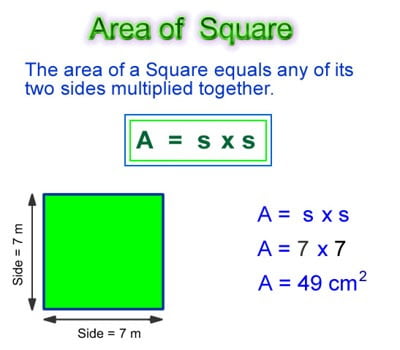
Look at the green square below. It covers 25 squares. So, the size in the area is approximately 25 sq units. In the diagram it is evident that each length is equal to 5 units. So, the square’s area each square represents the result of the product of the sides. The square’s area is equal to side + side = 5 x five = 25 units.

The area of the Square Formula

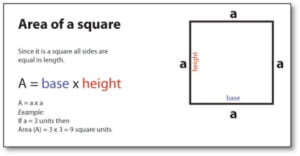
The formula to calculate the square’s area in the case of sides being given as follows: Area of a square = Side x Side = ^2.. Algebraically speaking, the square’s size can be determined by squaring the measurement of the square’s sides. Let us apply this formula to calculate the square’s area of 7 cm in size. We are aware that the square’s surface is Side + Side. By substituting the length of side 7 cm 7 7. So, the total area of the square given is 49cm ^2..

The square’s area is also determined by using that diagonal in the area. The formula to calculate the square’s size in the case of a diagonal is the following formula: Area of a square with the diagonal with Diagonal2/2. Let’s understand the underlying formula of this formula using the aid of the figure below where ‘d’ represents the diagonal, while’s is the side that make up the sides of the rectangle.

The part of the square that is’s’ while its diagonal is “d”. Utilizing the Pythagoras theorem, we get D2 = s2 + S2 2. the formula d = 2s and s = 2/2. The formula above will assist us in finding the area of the square by using the diagonal. Area = 2 = (d/2) ^2. = (d/2) ² = 2 = ^2./2. So, the area of it is equivalent to the ratio of ^2./2.

How to Determine the Area of a Square?

In the previous section, we discussed the definition of the term “area of square” and the area of the square formula. In this section , we will learn how to utilize an area formula to determine its area, with the aid of a handful of applications or actual examples.

Find the Area of a Square when the Square’s Perimeter is given

Examples: Find the area of an area of a square park, whose perimeter is 360 feet.
Solution
Given The perimeter of the square park = 360 feet
We are aware of that.
The square’s perimeter is 4xside
= 4 sides = 360
Side = 360/4
Side = 90ft
The area of a square is the side ²
Therefore, the Area of the park is 90% ^2. = 90 + 90 = 8100 ft ²
Therefore, the total area of a square park with a area is 360 feet is 8100 feet ^2..

Find the Area of a Square If the One Side of the Square is given

Examples: Find the area of a square park, whose the length is 90 feet.
Solution
Given side of square park = 90 feet
We are aware of that.
Square area = 2 feet ²
Therefore, the Area of the park is the square park is 90 ^2. = 90 x 90 = 8100 feet ²
So, the size that a park square, whose side is 90 feet is 8100 feet ^2.

Find the Area of a Square when the Diagonal of a square is given

Examples: Find the area of a square park, whose width is fourteen feet.
Solution
Square park’s Diagonal = 14 feet
We are aware of that.
Formula for calculating the area of a square when diagonal is calculated = 2/2/2/2/2/2/2. ²/2
Thus, the area of the park is (14 14 x 14)/2 = 98 feet ²
So, the square area of an area of a square park, with a diagonal of 14 meters is 98 feet ^2..

Important Notes about the Area of Square

Pay attention to the following factors that are important to remember when we determine the square’s area.

• The most common error that we often make when trying to calculate the square’s area is to double the square. This is not correct! Be aware that the square’s surface is side by side and not 2 sides.

• When we are describing the area, it is important to not forget to record the unit of measurement. The square’s side is one-dimensional, while the area of an area is two-dimensional. Therefore, the area of a square is described in square units. For instance, a rectangular square with a dimension of 3 units would comprise 3 (3 x 3) which is 9 sq units.

Example of the Area of a Square

1. 1. How big is the area of a rectangular swimming pool, whose side is equal to 8 meters?

   Solution

   We know that the length of one side of the pool is 8 meters therefore, we will apply the formula area of a square = side of 8 x side = 8 = 64 meters ^2.. So, the size of the area is 64 square metres.

2. Example 2.The surface of a square-shaped carromboard is 3600cm ^2.. Which is its length on its sides?

   Solutions:

   The area of the carrom square board = 3600cm ^2.. We are aware that Side = Area = Side = side ^2.. Therefore Side = Area = 3600 = 60cm. Thus, the length of the carrom board is 60cm.

3. Example 3.Find the size of the floor area that is square that is comprised from 100 rectangular tiles with a sides 15 inches.

   Solution

   One tile’s area is 15 inches x 15 inche sequals the area of 225 square feet. We can tell the existence of 100 tile covering floors of rooms. Therefore, the space occupied with 100 tiles represents called the floor surface. It is 100 square inches square inches x 225 sq inches or 22500 square inches. Thus, the total area on the floor will be 22500 sq. inches.

4. Example 4.Find the size of a carpet that’s the diagonal measures 4 feet.

   Solutions:

   The square’s area when its diagonal can be described as (D) ^2./2. If diagonal d is 4 feet. Carpet area is (4 + 4)/2 = 16/2, which is 8 sq. feet. So, the surface that the carpet covers is eight square feet.

FAQs regarding Area of Square

• What exactly is Area of Square in Geometry?

In the field of geometry, the square is a form with four sides of equal length. The square’s surface is the quantity of square units that comprise an entire square. It is determined by applying the formula of area of square Area = S x s = ^2, for square units.

• What is the Formula for finding The Area of a Square?

If the side of a square is identified The formula to determine the square’s size with a side’s’ Area = sx s = ^2.. If the diagonal that the square has is known then the formula used to calculate the area is area = ^2./2.

• How do you calculate the area of a Square?

The square’s area can be calculated using the aid of the formula area = sx S, which means that’s’ is the aspect that is a square. Because the square’s area is a two-dimensional number it is always calculated as square units. For instance, if you are trying to calculate the size of a rectangular square having sides of 4 units, the result will be A = 4 four = 16 units ^2.. Visit the the calculator for area of square to make easy calculations.

• What are What is Perimeter or Area of the Square Formulas?

Its length of an area is the combination of all four edges of the rectangle that equals P = Sides. It is expressed in terms of cm, m, feet, inches.
The square’s surface is s x s. In this case”s” is the an aspect of square. It is expressed in the form of 2 cm2, ft ² inches ² and Ft ² 2, in ^2..

Check Now:

• • Perimeter Formulas

  • Volume Formulas

  • Surface Area Formulas

  • Measurement Formulas

• How can I find what is the Area of a Square From the Diagonal of a Square?

It is possible to determine the surface that a rectangular area may be calculated when its diagonal is provided. The formula applied in this situation is an equation: Area of a sq. by using the diagonal = Diagonal2/2. For instance, if the diagonal of the square is 6 units and the area is 36/2 = 62/2 = 18 square units.

• How can I determine the area of a Square From the Perimeter of the Square?

The square’s area is calculated when its perimeter is identified. Because the square’s perimeter is P = 4xside and we can calculate the square’s side “s” = Perimeter/4. Once we have sides, the size of a given square can be calculated using the formula A = s * the square. In other words that the square’s perimeter has 32 units then we add this value to the formula P = 4x side. 32 = 4 sides. Therefore, the square would be eight units. We can now determine the size of the square with the side of 8 units. Area = s x s = 8 x 8 = 64 square units.

• What are the Units of the Area of a Square?

Since the size of the square is a two-dimensional shape, it’s defined in square units. most commonly used units for the area of the square are inches2, m2 cm2 foot2.

• What is the area of a Square Scripted in the form of a circle?

In the event that a square encased inside a circle dimension of that square will be the same as that of the size of the circle. If circles’ diameter is specified the value, it is used to calculate its diagonal for the sq and the square’s area is calculated using the formula area of a square by using the diagonals is Diagonal2/2.

www.GKDuniya.in will update many more new jobs and study materials and exam updates, keep Visiting and share our post of Gkduniya.in, So more people will get this. This content and notes are not related to www.GKDuniya.in and if you have any objection over this post, content, links, and notes, you can mail us at gkduniyacomplaintbox@gmail.com
And you can follow and subscribe to other social platforms. All social site links in the subscribe tab and bottom of the page.

Important Links

Check Other Post:- List of Chess Grand masters in India