Rational Numbers – gkduniya

Rational Numbers

Rational numbers are a popular type of number we typically study following the concept of integers in math. They’re in shape of p/q where p and Q can be any integer , and the q is 0. The majority of people find it difficult to distinguish the two types of numbers: fractions and rational numbers as a result of the fundamental structure of numbers, which is in the that of the p/q format. Fractions are composed of whole numbers, whereas rational numbers are composed of integers in the numerator as well as denominator. Learn the basics of rational numbers with this lesson.

How do you define Rational Numbers?

Do you know where the term “Rational” was derived? It’s derived in the term “ratio”. Therefore the rational numbers are closely related to the idea of ratio.

Rational Numbers Definition

Rational numbers are an numbers that has the form p/q in which the terms p and Q can be described as numbers and the sum of q is not the number 0. The rational number set is identified by the letter Q.

Also, if the number is described as a fraction, where the numerator and the denominator are integers, then the number is a rational one.

Examples of Rational Numbers

If a quantity can be represented as fractions, where both the numerator as well as the denominator are integers, then the number is considered to be a rational number. Examples of rational numbers include:

• 1/2

• 3/4

• 0.3 or 3/10

• -0.7 or 7/10

• 0.141414… (or 14/99).

Different types of rational numbers

There are many kinds of rational numbers. Don’t think that only integers in fractions constitute rational numbers. The different kinds of rational numbers include:

• integers like -2, 0, 3 etc.

• fractions with numerators and denominators that are integers such as 3/7, -6/5 and so on.

• terminating decimals like 0.35, 0.7116, 0.9768, etc.

• Non-terminating decimals with certain repetition designs (after that decimal mark) like 0.333 …, 0.141414 …, or 0.333 0.141414. They are commonly referred to as non-terminating decimals that repeat.

How can I identify Rational Numbers?

In all of these instances, the number could be expressed in terms of fractions of integers. Therefore every one of these numbers are rational numbers. To determine if a quantity is considered to be a rational one We can determine whether it is in line with one of the following conditions:

• The given number in fractions of integers

• We have the decimal extension of the number can be considered to be terminating or not repeating.

• All of the numbers that are whole are rational numbers.

Example: Is 0.923076923076923076923076923076… a rational number?

Solution:- The given number contains an array of decimals 923076 that is continuously repeating.

 

This makes it an univocal number.

Rational Numbers in decimal form

Rational numbers can have decimal representations. Do you know that 1.1 is an arbitrary number? It is true, because 1.1 could be expressed as 1.1equals 11/10. Let’s discuss non-terminating decimals like 0.333 ….. Because 0.333… could be expressed as 1/3 it’s a rational number. Therefore, decimals that are non-terminating and have repeated numbers following the decimal mark are rational numbers.

Does 0 count as a rational number?

Yes it is, the number 0 is a rational one since it is able to be written in fractions of integers such as 0/1, the 0/-2 ,… etc.

A List of Rational Numbers

Based on the information above it is evident that there exists an infinitum amount of numbers that are rational. This means that it is not possible to find the rational number list.

The smallest Rational Number

Because we are unable to identify the rational number list and therefore cannot find the number that is the smallest in rationality.

Points to Recall Rational Numbers

• Rational numbers aren’t just fractions but all numbers that is expressed in fractions.

• Whole numbers and natural numbers integers fractions of integers and decimals that end in a terminating point are all rational numbers.

• Non-terminating decimals that repeat pattern of decimals are rational numbers.

• If a fraction is marked with negative signs either to the numerator or the denominator, or even in front of it the fraction is considered to be negative. i.e the formula -a/b = A/B.

Arithmetic Operations Based on Rational Numeric

The rational numbers may be subtracted, added, multiplied, or split exactly like fractions. They are four most fundamental math operations applied to rational numbers..

• The addition of rational numbers

• Subtraction of rational numbers

• Multiplication of Rational Numbers

• Rational numbers are divided into rational divisions

Subtracting and adding Rational Numbers

Subtracting and adding rational numbers can be accomplished similarly to fractions. To subtract or add pair of rational numbers we create their denominators equal and then add their numerators.

Example: 1/2 + (-2/3)is 1/2+2/3 equals 1/2 3/3 + 2/3 2.2% = 2/6 4/6 = 6/6 = 1.

You can find out more about adding fractions as well as subtracting fractions.

Multiplying and Dividing Rationals

It is a process for multiplying and splitting rational numbers is done exactly the same way as fractions. In order to multiply any 2 rational number, you need to multiply their numerators and denominators individually and simplifies the resultant number.

Example: 3/5 x -2/7 = (3 x -2)/(5 7)= -6/35

To divide two fractions We multiply the first fraction (which is called dividend) with the reciprocal to the other fraction (which is divisor).

Example: 3/5 / 2/7=3/5 x 7/2 = 21/10 or 2110

Rational vs Irrational Numbers

The numbers that aren’t rational numbers are known as irresponsible numbers. The group of irresponsible number are represented in Q’. The distinction in rational and irresponsible number is as the following:

Rational Numbers	Irrational Numbers
These numbers can be expressed in fractions or integers. Examples: 0.75, -31/5, etc	These numbers cannot be expressed in fractions of integers. Examples: 5, p, etc.
They could be decimal endings.	They will never stop decimal numbers.
They may be non-terminating decimals that have repetitive pattern of decimals. Examples: 1.414, 414, 414 … is a repeating decimal patterns with 414 being the repeating.	They must be non-terminating decimals that do not have repeating pattern of decimal patterns. Example: 5 = 2.236067977499789696409173…. has no repeating patterns of decimals
The rational numbers set comprises all natural numbers, which includes all numbers in whole and all integers.	The number of numbers that are irrational is an entirely separate set, and is not part of the other sets of numbers.

Take a look at the chart below to comprehend the difference between rational and irrational numbers , along with other kinds of numbers visually.

Rational Numbers Examples

1. Example 1: Identify the rational numbers among the following: 4, 3, 5/2, -4/5, p, 1.41421356237309504…..

   Solutions:

   A rational number that is reduced must be either terminating or a non-terminating one with repeated patterns in decimals. The rational numbers within the numbers are -4/5 and 4/5.

2. Example 2 Find a rational number between 1/3 and 1/2.

   Solution

   We know that the mean of two numbers is between two numbers. Let’s find the median of two numbers that are rational.

   12+232=36+462=(76)2=(76)(21)

= 7/6 * 1/2
= 7/12

Therefore, the rationale number is 7/12.

Questions on Rational Numbers (FAQs on Rational Numbers)

• How do you define a rational number? Give an example.

Any number that has such a form as p/q, where the p and q represent integers and q does not equal to zero is an rational number. The most common rational numbers include 1/2, -3/4 0.3 or 3/10.

• What is the Rational Number?

To determine whether a number is rational, simply change it to decimal form. If the decimal ends or non-terminating and has repeating designs of the decimal the value is rational. In other cases, it’s not rational.

• What are Terminating Rational Counts?

Ending numbers with a terminating rational are decimal numbers that come to an end after a particular quantity of decimal numbers. For instance, 1.5, 3.4, 0.25 or 0.25 are all terminated numbers. The terminating numbers are all rational numbers since they are written as p/q in a snap.

• What is the difference between Rational Numbers and Irrational Numbers?

Rational numbers are non-terminating or terminating repeating numbers, while irrational ones are ones that don’t end nor repeat after a particular amount of decimal spaces.

• What is Irrational Numbers?

Irrational numbers are the ones that can’t be represented by integers using the p/q format. The set of numbers that are irrational is represented as Q’.

• Is 3.14 an accurate number?

It is true that 3.14 could be considered to be a rational number since it is an ending decimal. But take note that it is not an integer because the precise value of p does not equal 22/7. Its value is 3.141592653589793238… which has a decimal but no repeating patterns of decimals.

• Is 0 a rational number?

Yes that the number 0 is a rational one in the sense that we can write it as 0/1, where 1 and 0 are integers and the numerator does not correspond to the number 0.

• What is the number that is added to Pi to get the Rational Number?

If we add p to p, we’ll get the sum – p + = zero. This is an rational number. Thus, by adding by p we will get the rational number.

• How do I Use Rational Numbers Calculator?

Rational number calculator can be a web-based tool that can be used to calculate rational numbers that are between two numbers. A rational number has formula ‘p/q’ in which ‘p’ is an integer, and “q” is a non-zero value. Check it out now Cuemath’s online rational numbers calculator to calculate the rational number in two numbers quickly and in only a few seconds.

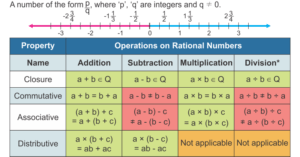
• What is the Properties of Rational Numbers?

  • The six characteristics that rational numbers possess that are described below:

    • Closure Real Property of Rational Numbers

    • Compmutative Property of Rational Numbers

    • The Associative Property Rational Numbers

    • The Distributive Property Rational Numbers

    • Multiplicative property of Rational Numbers

    • Additive Property of Rational Numerics

 

www.GKDuniya.in will update many more new jobs and study materials and exam updates, keep Visiting and share our post of Gkduniya.in, So more people will get this. This content and notes are not related to www.GKDuniya.in and if you have any objection over this post, content, links, and notes, you can mail us at gkduniyacomplaintbox@gmail.com
And you can follow and subscribe to other social platforms. All social site links in the subscribe tab and bottom of the page.

Important Links

Particulars Official Links	Related Links
Official Site	View more at website
You-tube	GKDuniya9
Instagram	GKDuniya.in,   IndiaDigitalHub
Facebook	GKDuniya.in
Another site visit	Indiadigitalhub.com
Get new updates	Click here

Check Other Post:- 11 October 2021 Current Affairs