NCERT Solutions for Class 10 Maths Chapter 1

NCERT Solutions for Class 10 Maths Chapter 9 त्रिकोणमिति के कुछ अनुप्रयोग – टर्म II

यह अध्याय पिछले अध्याय की निरंतरता है क्योंकि यहां छात्र के अध्ययन करेंगे त्रिकोणमिति अनुप्रयोगों का । इसका उपयोग भूगोल, नेविगेशन, मानचित्रों के निर्माण, देशांतर और अक्षांश के संबंध में एक द्वीप की स्थिति का निर्धारण करने में किया जाता है। इस अध्याय में, छात्र यह देखेंगे कि विभिन्न वस्तुओं की ऊंचाई और दूरी को खोजने के लिए त्रिकोणमिति का उपयोग कैसे किया जाता है, वास्तव में उन्हें मापे बिना। उन्हें दृष्टि रेखा, उन्नयन कोण, अवनमन कोण से परिचित कराया जाएगा।

कक्षा 10 गणित अध्याय 9 में शामिल विषय टर्म II के लिए त्रिकोणमिति के कुछ अनुप्रयोग:

ऊंचाई और दूरी-ऊंचाई का कोण, अवसाद का कोण।
ऊंचाई और दूरियों पर साधारण समस्याएं। समस्याओं में दो से अधिक समकोण त्रिभुज शामिल नहीं होने चाहिए। ऊंचाई/अवनमन कोण केवल 30°, 45°, 60° होना चाहिए।

महत्वपूर्ण बिंदु –

दृष्टि की रेखा प्रेक्षक की आंख से प्रेक्षक द्वारा देखी गई वस्तु के बिंदु तक खींची गई रेखा है।

देखे गए बिंदु का उन्नयन कोण क्षैतिज के साथ दृष्टि की रेखा द्वारा निर्मित कोण होता है जब देखा जा रहा बिंदु क्षैतिज स्तर से ऊपर होता है, अर्थात, वह स्थिति जब हम वस्तु को देखने के लिए अपना सिर उठाते हैं।

देखी जा रही वस्तु पर किसी बिंदु का अवनमन कोण क्षैतिज के साथ दृष्टि रेखा द्वारा निर्मित कोण होता है जब वह बिंदु क्षैतिज स्तर से नीचे होता है, अर्थात वह स्थिति जब हम देखे जा रहे बिंदु को देखने के लिए अपना सिर नीचे करते हैं।

NCERT-Solutions-for-Class-10-Maths-Chapter-9-Minar, GKDUNIYA

आपको निम्नलिखित जानने की आवश्यकता होगी:

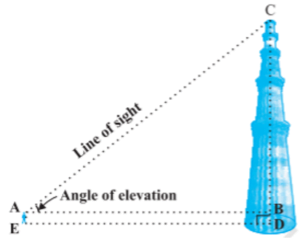
(i) दूरी DE जिस पर छात्र मीनार के पैर से खड़ा है

(ii) मीनार के शीर्ष का उन्नयन कोण, BAC,

(iii) छात्र की ऊंचाई AE।

यह मानते हुए कि उपरोक्त तीन स्थितियां ज्ञात हैं, हम मीनार की ऊंचाई कैसे निर्धारित कर सकते हैं?

• आकृति में, सीडी = सीबी + बीडी। यहाँ, BD = AE, जो विद्यार्थी की ऊँचाई है।
• BC ज्ञात करने के लिए, हम BAC या A के त्रिकोणमितीय अनुपातों का उपयोग करेंगे।
• ABC में, ज्ञात ∠ A के संबंध में भुजा BC विपरीत पक्ष है। हमारी खोज या तो tan A या cot A का उपयोग करने तक सीमित है, क्योंकि इन अनुपातों में AB और BC शामिल हैं।
• इसलिए, tan A = BC/AB या cot A = AB/BC, जिसे हल करने पर हमें BC प्राप्त होगा।
• AE को BC में जोड़ने पर आपको मीनार की ऊंचाई मिल जाएगी।

NCERT Solutions for Class 10 Maths Chapter 10 वृत्त – टर्म II

पिछली कक्षाओं में, छात्रों ने एक एक वृत्त वृत्त और से संबंधित विभिन्न पदों जैसे जीवा, खंड, चाप, आदि के बारे में अध्ययन किया है। इस अध्याय में, छात्र उन विभिन्न स्थितियों का अध्ययन करेंगे जो एक वृत्त और एक रेखा को एक में दिए जाने पर उत्पन्न होती हैं। विमान। इसलिए, वे एक वृत्त पर स्पर्शरेखा और एक वृत्त पर एक बिंदु से स्पर्शरेखाओं की संख्या की अवधारणा से पूरी तरह परिचित होंगे।

कक्षा 10 गणित अध्याय 10 में शामिल विषय टर्म II के लिए वृत्त:

वृत्त की स्पर्श रेखा, संपर्क बिंदु पर
1. (सिद्ध करें) वृत्त के किसी भी बिंदु पर स्पर्श रेखा संपर्क बिंदु से जाने वाली त्रिज्या पर लंबवत होती है।
2. (सिद्ध करना) किसी बाहरी बिंदु से वृत्त पर खींची गई स्पर्श रेखाओं की लंबाइयाँ बराबर होती हैं।

महत्वपूर्ण प्रमेय –

प्रमेय 10.1: वृत्त के किसी भी बिंदु पर स्पर्श रेखा संपर्क बिंदु से जाने वाली त्रिज्या पर लंबवत होती है।

प्रमेय 10.2: किसी बाहरी बिंदु से वृत्त पर खींची गई स्पर्श रेखाओं की लंबाई बराबर होती है।

एक वृत्त पर एक बिंदु से स्पर्श रेखाओं की संख्या

स्थिति 1: वृत्त के अंदर स्थित एक बिंदु से गुजरने वाले वृत्त की कोई स्पर्श रेखा नहीं है।

स्थिति 2: वृत्त पर स्थित एक बिंदु से गुजरने वाले वृत्त की एक और केवल एक स्पर्श रेखा होती है।

स्थिति 3: वृत्त के बाहर स्थित एक बिंदु से वृत्त पर ठीक दो स्पर्श रेखाएँ होती हैं।